⚡참고: GitHub - VSFe/Tech-Intervicew

🤐 세부 질문

1️⃣ Quick Sort와 Merge Sort를 비교해 주세요.

2️⃣ Quick Sort에서 O(N^2)이 걸리는 예시를 들고, 이를 개선할 수 있는 방법에 대해 설명해 주세요.

3️⃣ Stable Sort가 무엇이고, 어떤 정렬 알고리즘이 Stable 한지 설명해 주세요.

4️⃣ Merge Sort를 재귀를 사용하지 않고 구현할 수 있을까요?

📢 키워드별 설명

1️⃣ Quick Sort와 Merge Sort

Quick Sort

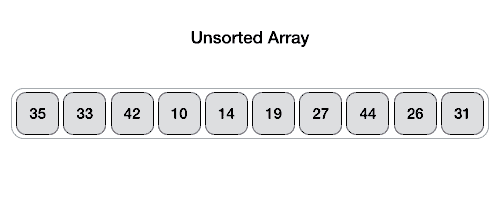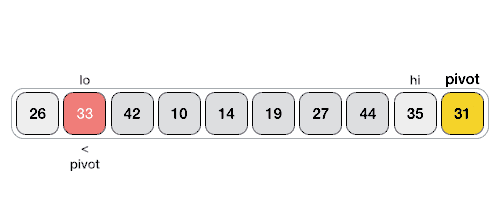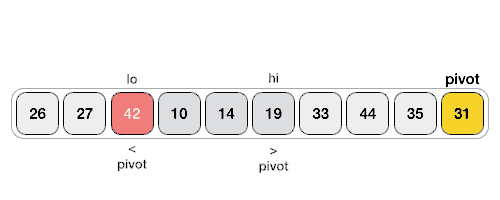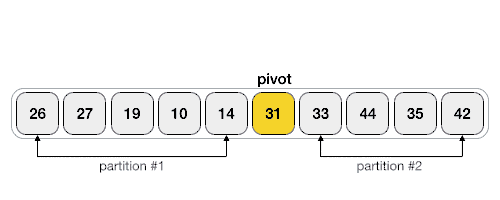
: 하나의 Pivot을 선정 → 이 값을 기준으로 정렬을 해나감. 예를 들어 Pivot보다 작은 값은 좌측, Pivot보다 큰 값은 우측에 위치시키도록 한다 ( 우측 .gif은 1회의 작업만을 나타냄, 이후 분할된 부분 집합에서 재진행)

(ft. 분할 정복 알고리즘)

알고리즘적 특징

In-place	배열을 나누는 과정에서 나누어진 배열을 별도로 저장할 공간이 불필요함 그러나, 별도의 메모리 공간이 필요하도록 구현하는 방법도 존재
UnStable	같은 값의 데이터의 기존 순서 유지를 보장 불가 그러나, stable 알고리즘으로 구현하는 방법도 존재

시간최상	시간평균	시간최악	공간
O(nlogN)	O(nlogn)	o(n^2)	o(n)

Merge Sort

: 기존의 배열을 반으로 지속적으로 나누어 1개만 남을 때까지 분할, 그 뒤 다시 정렬해가며 하나로 합치는 방식

(ft. 분할 정복 알고리즘)

알고리즘적 특징

Not In-place	배열을 합치는 과정에서 나누어진 배열을 별도로 저장할 공간이 요구됨
Stable	같은 값의 데이터의 기존 순서 유지를 보장 가능

시간최상	시간평균	시간최악	공간
O(nlogN)	O(nlogn)	o(nlogn)	o(n)

2️⃣ Quick Sort에서 O(N^2)이 걸리는 예시를 들고, 이를 개선할 수 있는 방법에 대해 설명해 주세요.

Quick Sort의 최악의 경우, O(N^2)

우선, 일반적으로 pivot의 자리를 결정하는 것이 맨 끝이나 맨 뒤와 같이 고정적이다
첫 Index를 Pivot로 하고 그 뒤로 내림차순으로 들어온 자료에 대하여 오름차순 정렬을 하려할 경우가 그 예다. 설명으로는 다음과 같다.

1. 오름차순 정렬을 목적으로, index:0을 pivot으로 설정하였다
이때, 나머지 index:1~9는 내림차순으로 정렬되어있다

2. Pivot은 본인보다 큰 값을 찾지 못하고, 배열의 남은 index만큼을 다 돌고서 마지막에 도착한다

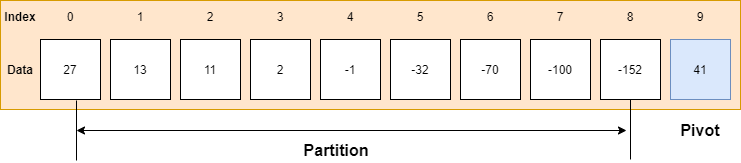
3. 이후, 27은 다시 pivot이 되어 마지막 인덱스까지 돌게 될 것이며 나머지도 이와같이 진행된다
따라서, $O(N^2)$ 최악의 시간복잡도 발생

🍊 이때, 앞서 말한 Pivot의 고정적 자리 결정방식의 변화가 이에 대한 해결책이 될 수 있다

Quick Sort의 최악의 시간복잡도 개선법

sol1. Random한 자리 결정방식

단순히 랜덤하게 Pivot의 자리를 결정시킨다면 항상 최악의 Case가 발생하지는 않을 것이다
단, ‘항상’이 아닐 뿐 최악의 case는 생길 수 있다
평균적으로는 O(n*logN) 시간복잡도를 유지할 가능성이 크다

sol2. Median-Of-3 Method

배열의 값들 중 가장 좌측/우측/중앙값 3가지를 뽑는다
- 이후, 3개의 값을 우선적으로 정렬한 뒤 그 중 중간값을 가장 좌측 또는 우측으로 이동시켜 Pivot으로 설정한 뒤 퀵 정렬을 수행하도록 만든다
이 값은 Pibot으로 사용되어 전체 배열을 균등하게 분할할 것이라는 보장은 없지만, 최소한 이 값이 전체 값 중 최대, 최소값에는 해당하지 않는다
중심 극한 정리에 따라 평균적으로 O(n*logN)의 시간복잡도를 유지할 수 있어진다

위 과정에 대한 예시는 다음과 같다

index	0	1	2	3	4	5	6	7	8	9
value	35	3	42	10	14	19	27	44	26	31

1. First:35, Middle:14, Last:31 이다

2. 정렬결과, 35 31 14가 된다

3. 새롭게 middle값을 차지한 31을 pivot으로 하여 Quick-Sort를 진행한다

private static int get_median(int[] arr, int start, int end){
        // end 값이 현재의 length 혹은 이전 pivot index 이므로 1을 빼준다.
        int center = (start+end)/2;

        // 3개의 값을 크기 순서대로 정렬해서 Low / Median / High의 순서로 만든다.
        if(arr[start] > arr[center])
            swap(arr, start ,center);

        if(arr[start] > arr[end-1])
            swap(arr, start, end-1);

        if(arr[center] > arr[end-1])
            swap(arr, center, end-1);

        // 정렬된 상태에서 마지막과 중간을 교환하여 중간값을 최 좌측으로 이동시킨다.
        swap(arr, start, center);
        return arr[start];
    }

    private static void swap(int[] arr, int i, int j) {
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }

3️⃣ Stable Sort가 무엇이고, 어떤 정렬 알고리즘이 Stable 한지 설명해 주세요.

StableSort & UnSatbleSort

Stable: 같은 숫자라도 그 상대적인 위치가 유지되는 sort방식
StableSort의 예시는 다음과 같다
- 3 3 4 2 1 4 3
- 1 2 3 3 3 4 5 (Safe Sorting)

Sort기법 별 Stable 사항 (Notion 정리 사진으로 대체)

표만들기 힘들어잉

🍊 Safe → Unsafe, UnSafe → Safe하게 커스텀하는 건 항상 가능할까?

: 보편적으로 safe → Unsafe 방향의 커스텀은 쉬운 편이다. 그러나, 그 반대방향은 까다롭고 복잡하다. 예를 들어 퀵 정렬의 경우는 계속해서 앞뒤가 바뀌는데 이를 위해선 원래 순서를 기억하게 만들거나 다른 정렬 기법을 하이브리드 시키는 보다 어려운 방법을 요구하게 된다.

결론적으로 모든 정렬 알고리즘을 뒤집어서 만들 수는 없고, 어느 정도의 필요에 따른 커스텀은 가능하다.

Stable Sort의 필요성

원하는 결과값, 특히 key-value형태로 조회한다고 생각해보자

🍊언뜻 보기에는 key에 대해서는 잘 되어있지만 상황에 따라 value의 오름차순이 필요한 경우도 있을 것이다. 그것이 보장되지 않는다면 후의 재사용성이 떨어질 수 있다

🍊 safe를 보장하는 것이 좋을텐데 굳이 Unsafe로 만들지 않는 이유가 있을까?

: 알고리즘 선택시 ‘안정성’ 외에도 여러 가지 요소를 고려하기 때문에, 굳이 ‘safe’하게 유지하지 않으려는 것이다. 라는 게 답변에 어울린다. 그리고 알고리즘 선택시 고려해야할 요소와 그에 따른 Unsafe 알고리즘 선택 이유는 다음과 같다

성능: 안정성을 유지하려고 하면 추가적인 시간적, 공간적 복잡도를 가지는 경향이 있다
메모리 사용량: Unsafe정렬 알고리즘은 in-place성질을 같이 가지는 경향이 있으며, 추가적인 메모리를 사용하지 않아도 된다는 것이다
구현 복잡성: 안정성을 위해선 추가적인 구현 비용이 든다

4️⃣ Merge Sort를 재귀를 사용하지 않고 구현할 수 있을까요?

일반적인 Merge sort 구현방법

이론

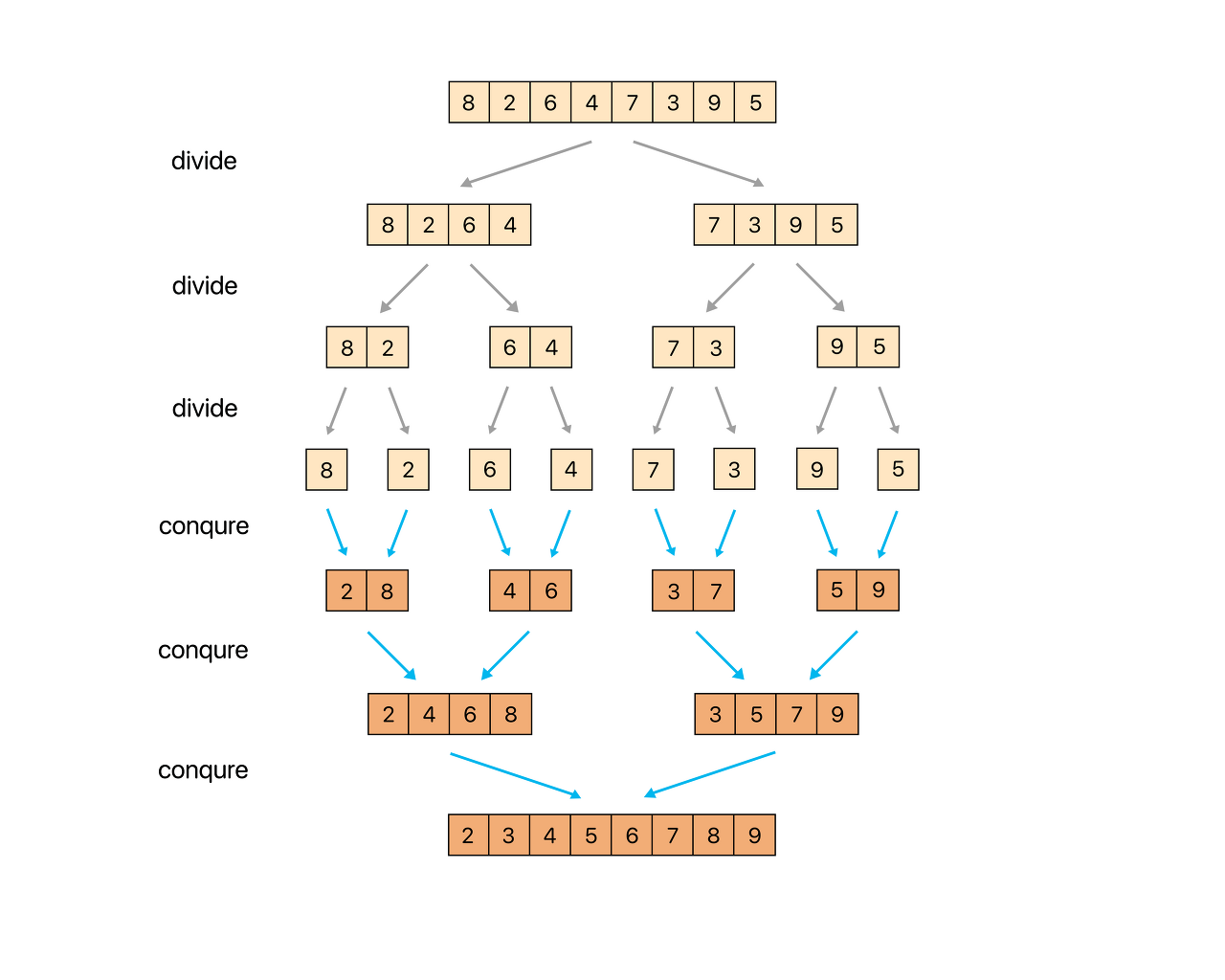
주어진 리스트를 절반으로 분할하여 부분리스트로 나눈다
해당 부분리스트의 길이가 1이 아니라면 1번 과정을 되풀이한다 (재귀)
인접한 부분리스트끼리 정렬하여 합친다

code : 재귀로 구현하기 (Top-Down)

// 부분리스트를 계속해서 나누고 있음
private static void merge_sort(int[] a, int left, int right) {

        if(left == right) return;

        int mid = (left + right) / 2;    // 절반 위치 

        merge_sort(a, left, mid);        // 절반 중 왼쪽 부분리스트(left ~ mid)
        merge_sort(a, mid + 1, right);    // 절반 중 오른쪽 부분리스트(mid+1 ~ right)

        merge(a, left, mid, right);        // 병합작업 (생략)

    }

code: 비재귀적으로 구현하기(Down-Top)

private static void **merge_sort**(int[] a, int left, int right) {

        /*
         * 1 - 2 - 4 - 8 - ... 식으로 1부터 서브리스트를 나누는 기준을 두 배씩 늘린다.
         */
        for(int size = 1; size <= right; size += size) {


              //두 부분리스트을 순서대로 병합해준다.
              //예로들어 현재 부분리스트의 크기가 1(size=1)일 때
              //왼쪽 부분리스트(low ~ mid)와 오른쪽 부분리스트(mid + 1 ~ high)를 생각하면
              //왼쪽 부분리스트는 low = mid = 0 이고,
              //오른쪽 부분리스트는 mid + 1부터 low + (2 * size) - 1 = 1 이 된다.

              //이 때 high가 배열의 인덱스를 넘어갈 수 있으므로 right와 둘 중 작은 값이
              //병합되도록 해야한다. 

            for(int l = 0; l <= right - size; l += (2 * size)) {
                int low = l;
                int mid = l + size - 1;
                int high = Math.min(l + (2 * size) - 1, right);
                **merge**(a, low, mid, high);        // 병합작업
            }
        }