[자료구조] 우선순위 큐의 자료구조는 뭘까

 

 

 

 

알다시피 힙을 쓴다

기존의 Queue는 먼저 들어온 것이 먼저 나가는 FIFO 구조였다. 여기에 우선순위라는 조건이 더해져, 해당 우선순위가 높은 원소부터 나가는 것이 PriorityQueue다. 그렇다면 이 PriorityQueue(이하 PQ)는 원소의 추가가 일어날때마다 우선순위 조건에 대한 정렬상태를 잘 유지해야 할 것이고, .poll()을 진행할 시 최댓값이나 최솟값에 대해 빠르게 접근하여 가져와야 할 것이다.

위와 같은 고려를 하고보니 Heap이 제일 적절하더라인데, 조금만 더 살펴보자.

 

배열로 구현하면 어디서 문제인가

 

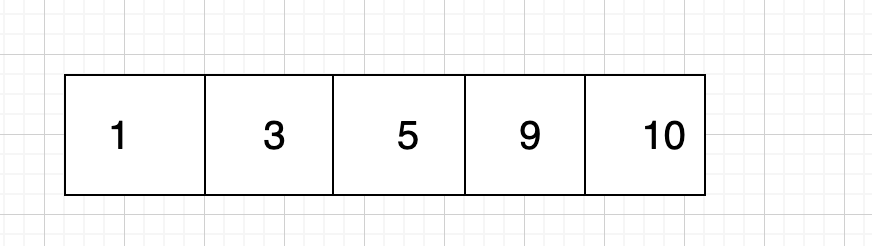
최솟값에 따라서 정렬된 상태를 배열로 관리하고 있다고 치자, 당연히 배열이니까 최솟값인 첫 자리에만 접근하는 탐색 비용은 O(1)이다.

 

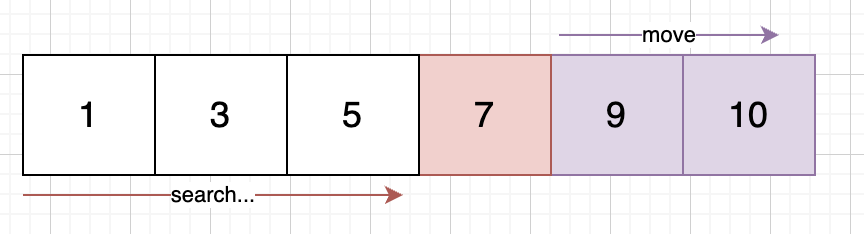
하지만 이제 '7'이라는 숫자가 들어와 정렬상태를 바꾸려고 하면 7의 위치를 찾기 위한 탐색 비용과 더불어 이후 [9], [10]은 연쇄적으로 자리의 밀려나야한다. 따라서, 삭제에 대한 O(1)과 반비례하는 삽입에 대한 O(n) 시간복잡도로 비효율적임을 알 수 있다.

 

연결리스트로 구현하면 어디서 문제인가

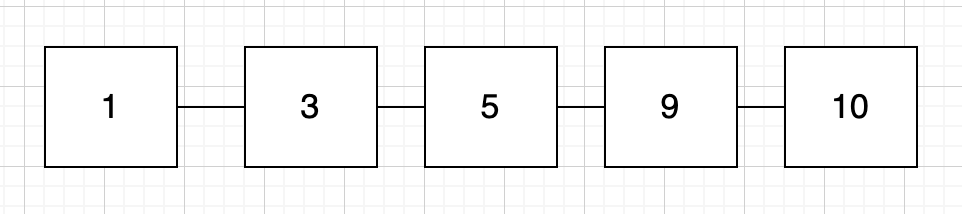
배열과 크게 다르지 않다. 정렬된 상태에서 첫 자리에만 접근한다면 탐색 비용은 O(1)로 빠르다.

그러나 마찬가지로 이 7의 원소가 들어갈 자리를 알고자 한다면 최악의 경우 O(n) 시간복잡도로 비효율적임을 알 수 있다

 

 

힙으로 구현하면 어떤가

앞서서 배열이든 연결리스트든 삽입되는 원소의 자리를 찾는데에 비효율적인 것이 문제점일을 알았다.

그렇다면 이 검색에 대한 문제를 개선시키기 위해, 우리는 Tree 구조를 갖춘 Heap를 쓰는 게 낫다는 걸 떠올릴 수 있다

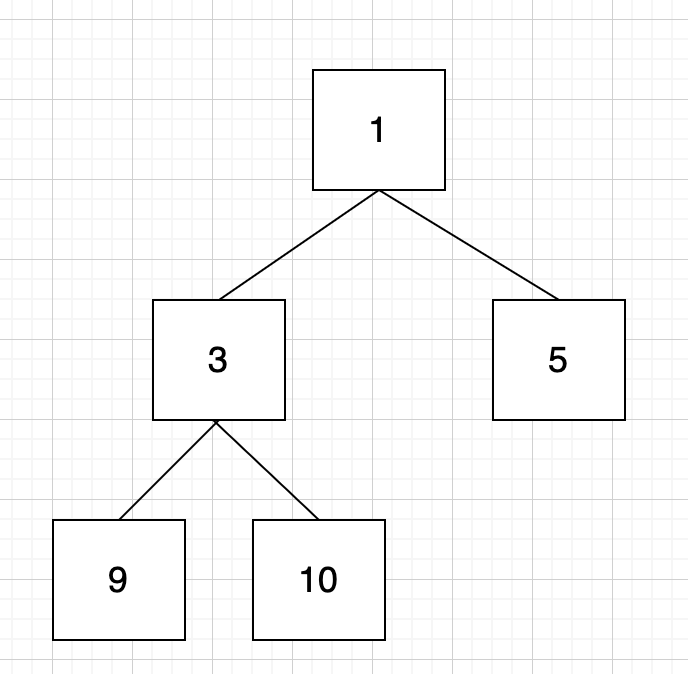
입력되는 순서에 따라 이렇게 생긴 트리가 기존에 구성되었고 이 상태에서 7을 삽입하기 위해선 아래와 같다.

 

 

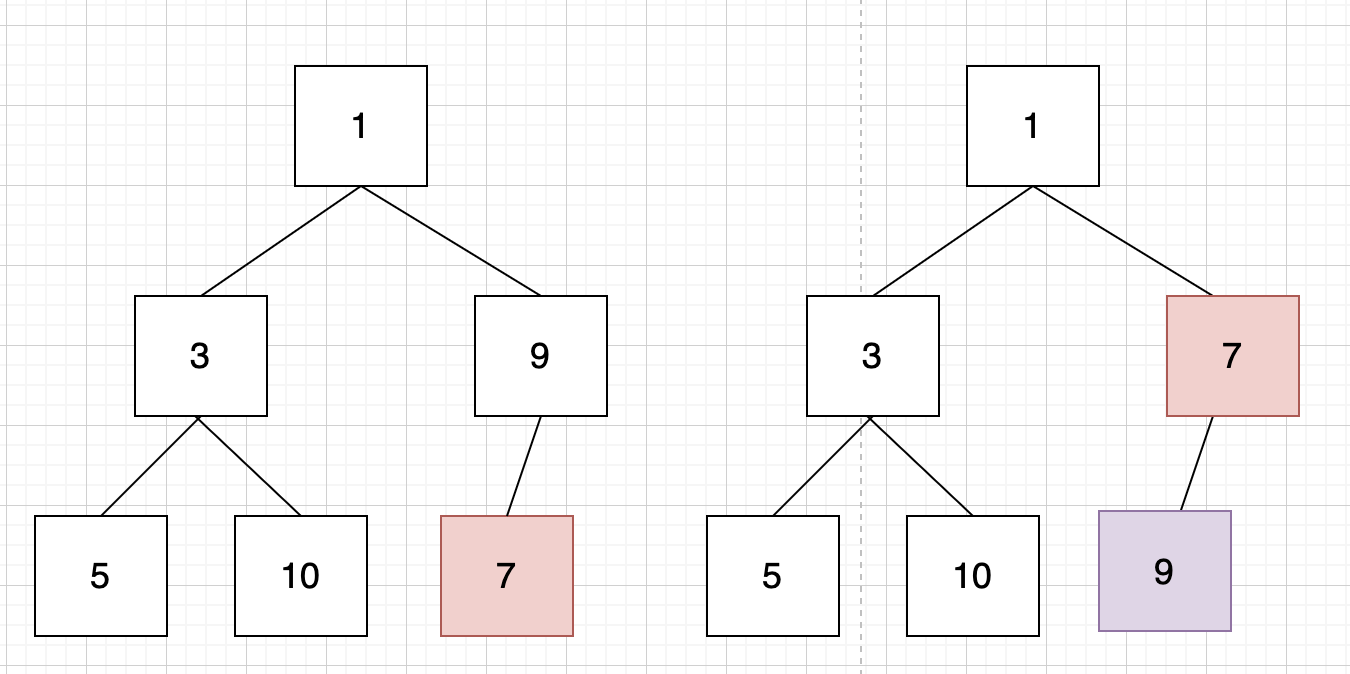
일단 달아놓고 상위 노드가 우선순위 조건에 대해서 대소를 구분하여 이동을 시키면 되는 것이다.

 

 

힙의 구현 자체는 배열로 구현해도 된다

세그먼트트리 알고리즘을 사용하는 사람은 이미 알다시피, 완전이진트리 구조는 배열로 그 자리를 명확히할 수 있다.

 

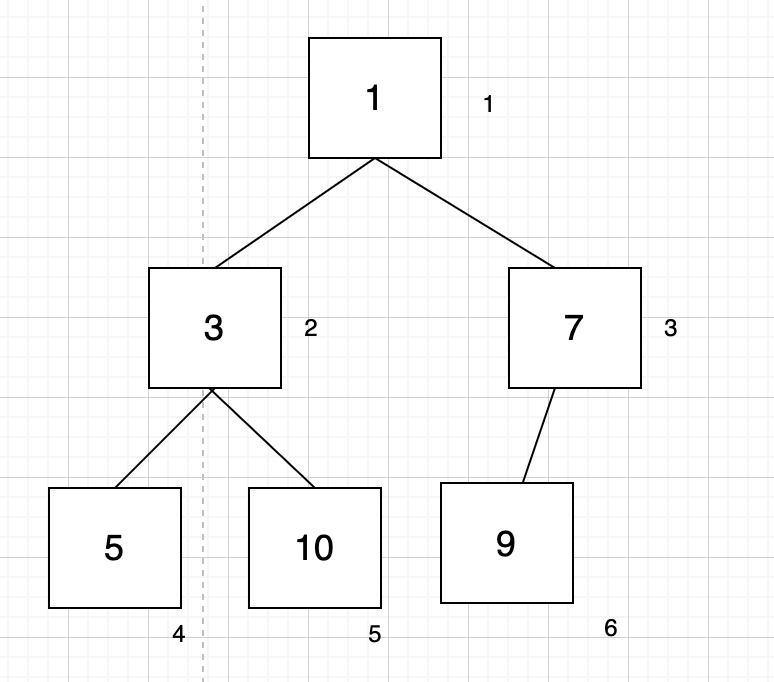
그린 것 처럼 [1]자리는 하위 자식노드의 번호로 [2], [3]을 가질 수 있고, [2]는 [4],[5]를 가질 수 있으며 [3]은 [6],[7]을 가질 수 있게끔 되어있다. 그러니, 배열에서 [i]의 하위 노드가 [2*i]와 [2*i+1]을 각각 좌, 우를 나타냄을 눈치챈다면 heap[] 이라는 사실상 배열의 구조를 통해 구현할 수 있는 것이다.

 

 

 

 

 

 

Reference

자료구조 - 우선순위 큐(Priority Queue)와 힙(heap)