
행렬의 연쇄 곱셈이란
여러 행렬의 곰센 순서를 최적화하여 문제를 해결하는 알고리즘이다. 이 알고리즘은 해열 곱셈 연산의 횟수를 최소화하기 위해 사용된다. 우선 행렬 곱셈부터 다시 점검해보면 아래와 같다.
행렬 곱셈의 결합법칙

사전적으로, 행렬 A와 B의 곱이 정의되기 위해서는 위와 같이 A행렬의 열과 B행렬의 행의 크기는 같아야한다.
(더불어 A*B 결과인 X행렬은 (A행렬의 열크기) x (B행렬의 행크기), 즉 p*r이 된다.)

열과 행의 조건을 성립한 행렬의 곱셈은 연산 순서자체는 결과에 영향을 미치지 않는다.

하지만 과정에서 차이가 있다. 연산 횟수에 대한 공식 자체는 위와 같다.
A의 한 행과 B의 한 열이 곱해져서 C의 하나의 원소를 계산하기 때문에, 한 원소를 계산하기 위해선 'q'번의 곱셈이 필요하다. 그리고 결과 행렬 X는 p*r개의 원소가 있을 테니 이를 곱해주면 총 연산 횟수가 결정된다.
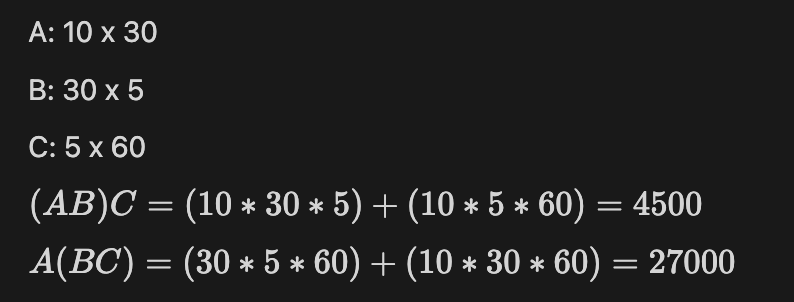
따라서 연산 횟수 공식을 대입해보면, A*B*C 행렬은 그 결합순서에 따라 횟수에 대해 영향을 미친다.
위처럼 연산 횟수의 자릿수 자체가 바뀌는 수준이기에 행렬의 크기가 크거나 곱의 개수가 많아질수록 적절한 곱셈 순서를 찾는 것이 중요하다
행렬의 연쇄 곱셈 알고리즘으로 풀기
맨 앞에서 정의한 바와 같이 목표는 연산의 최소화다. 즉, 아래와 같이 분석할 수 있다.
1. 여러 개의 행렬을 곱하는 최적의 순서를 찾아야 한다
2. 단순히 순열로 모든 경우를 계산하면 이에 대한 알고리즘 수행 속도가 지나치리 크다 (O(n!))
3. 행렬 A1, A2, A3... 를 곱하는데 필요한 최소 계산량을 구하려면 어떻게 해야하나?
3번을 상세화 해보자.
최소 계산량을 어떻게 해야하나?
일단 작은 단위로 분할해본다

cal[1][n] = cal[1][k] + cal[k+1][n] 로 나타낼 수 있다 ( cal[][]: 최소 연산횟수에 대한 이차원 배열)
그리고 일반화 시켜보면
cal[i][j] = cal[i][k] + cal[k+1][j] + 현재 곱셈 비용
(k는 이를 최소로 만드는 값, 현재곱셈비용= P(i-1) * P(k) * P(j))
그리고 이 연산에서 생각해보면 중간에 사용되는 값이 중복되고 있다

위 트리의 노드가 뻗어나가면 이렇게 겹치는 연산에 대한 값이 무조건 생길테니 말이다.
그러니 결론적으로 DP, 즉 동적게획법을 풀이법으로 생각할 수 있다.
DP 테이블 설계하기
동적계획법을 쓰기로 했으니, DP로 사용할 결과 테이블을 생각해보자
cal[i][j]는 Ai부터 Aj까지 곱하는 최소 계산량을 나타낸다.
초기화
행렬 한 개를 곱하는 데는 계산이 필요없다.
m[i][i] = 0이다.
점화식
cal[i][j] = cal[i][k] + cal[k+1][j] + p[i-1]*p[k]*p[j]
이때, k는 i와 j의 사이값으로서, 이 값을 최소로 만드는 애를 찾아와야한다.
결과값
cal[0][n-1] 이다.
완전탐색으로 K를 찾기
완전탐색으로 k를 찾아 최솟값을 찾아본다
입력은 각 행렬의 행 길이, 열 길이가 N번 들어온다고 쳤을 때이며, 이제 cal을 dp라고 부르자.
int N = Integer.parseInt(br.readLine());
int[][] arr = new int[N][2];
for (int i = 0; i < N; i++) {
st = new StringTokenizer(br.readLine());
arr[i][0] = Integer.parseInt(st.nextToken()); //
arr[i][1] = Integer.parseInt(st.nextToken());
}
dp = new long[N][N];
for (int cnt = 2; cnt <= N; cnt++) { // 행렬의 곱 횟수
for (int i = 0; i < N - cnt + 1; i++) {
// 가장 작은 단위부터 수행, 'i-j = 1' 부터 시작
int j = i + cnt - 1;
dp[i][j] = Long.MAX_VALUE; // 최솟값 갱신을 위한 초기값
for (int k = i; k < j; k++) {
// arr[i][0] = p, arr[k][1] = q, arr[j][1] = r
long cost = dp[i][k] + dp[k + 1][j] + (arr[i][0] * arr[k][1] * arr[j][1]);
dp[i][j] = Math.min(dp[i][j], cost);
}
}
}
이제 아래의 문제를 풀 수 있다.
https://www.acmicpc.net/problem/11049

